Diagnostics of mathematical development of older preschool children
Diagnostics of mathematical development of older preschool children
Theoretical part:
1.Diagnostic functions in preschool mathematics education
Diagnostics in preschool mathematics education can be of two types: express diagnostics and system diagnostics. Each of these types of diagnostics has its own functions.
Express diagnostics
– This is a one-time examination, usually carried out independently of the pedagogical learning process. The functions of this type of diagnosis are to give a fairly current picture of the child’s level of mathematical development today, as well as the “zone of proximal development.” Express diagnostics determines a complex of internal mental and external environmental factors. Another function of express diagnostics is to determine the current level of mathematical development of a child entering first grade.
System diagnostics –
This is the systematic “tracking” of a child by a teacher in the process of systematically working with him. The functions of system diagnostics make it possible, based on its results, to build a long-term forecast for the development of a child’s mathematical abilities. There is also a function for tracking the individual “speed” of progress in mathematical development and predicting the child’s zone of proximal development. Systemic diagnostics is an integral part of the process of learning and development of a child. In the process of systematic educational work with a child, built on the principles of developmental education, all areas of development (intellectual, emotional, social, physical, etc.) are in the sphere of constant attention and observation of the teacher and psychologist. The function of tracking a child’s mathematical development allows you to provide the necessary assistance in a timely manner, both for the purpose of correcting and compensating for development, and for the purpose of preventing further school maladjustment.
Pedagogical diagnostics is a mechanism for identifying individual characteristics and prospects for personal development. With the help of pedagogical diagnostics, the educational process is analyzed and the results of the activities of both the child and the teacher are determined. The goal of diagnostics is to obtain more complete information about the individual characteristics of children’s development, on the basis of which recommendations can be developed for educators, psychologists, and parents to prepare children for school and select the optimal forms of further education at the stage of primary general education.
Diagnostic functions:
analytical –
identifies cause-and-effect relationships in the educational process between conditions and learning outcomes;
actually diagnostic
– contributes to the study of the level of training, education and development of the child, as well as the level of professional competence of the teacher;
evaluative
– involves qualitative and quantitative assessment of the activities of participants in the pedagogical process;
correctional
– aimed at correcting (changing) the actions of the teacher and the child in order to eliminate the negative consequences of learning;
orientational
– provides for the prevention of negative consequences of training and the identification of new goals;
informational
– aims to constantly inform participants in the pedagogical process about the positive results of pedagogical diagnostics.
2. Methodology for diagnosing the level of mathematical development of a child
The purpose of diagnostics is to monitor children’s mastery of the basic methods and techniques of cognitive (mathematical) activity, practical actions, content, verbal expression of methods and results of practical and mental actions. During the diagnosis, the attitude of children to cognitive and creative mathematical tasks is clarified: delight and maximum activity or indifference; the ability to show creativity or the desire to simply reproduce a given task, etc.
Diagnostics are carried out based on the following indicators of three expected levels of children’s mastery of mathematical content:
— the child’s mastery of the practical actions of comparison, equalization, counting, calculations, measurement, classification and seriation, modification and transformation, etc.;
- the nature of children’s ideas about relationships, dependencies of objects in size, quantity, shape, location in space, etc.;
- level of verbal expression of methods of practical actions: use of terminology, structure and construction of sentences, originality and accuracy of statements;
— the degree of independence and creative manifestations in the course of mastering and transferring mathematical knowledge and skills to new conditions.
As an example, I propose a method for diagnosing the mathematical development of children of middle preschool age (compiled by I.N. Cheplashkina, L.Yu. Zueva - St. Petersburg, “Accent”, 200 6).
The tasks are aimed at identifying the following skills:
- determine the shape, recreate the figure from parts (elements);
- use numbers: count, equalize, navigate in numbers;
- move through the labyrinth;
- solve logical problems, show guesses, explain your actions.
Criteria for development levels
- Perception, selection, selection of shapes (square, rectangle, triangle), recreating them from elements (parts).
Low level.
Highlights, names figures (confuses names). Doesn't have the ability to recreate. Names individual words.
Average level.
Identifies and names figures. Doesn’t know how to recreate (makes certain attempts). The actions are explained schematically.
High level.
Selects, names figures, explains actions. Recreates geometric shapes from parts.
- Ability to determine quantity using numbers; practically establish equality, distinguish, name numbers, their sequence.
Low level.
Determines quantity, makes mistakes in using numbers after four, distinguishes numbers. Does not establish equality.
Average level.
Uses numbers accurately, distinguishes and partially names numbers, does not establish equality, explanations are fragmentary.
High level.
Uses numbers accurately, knows the sequence of numbers, equalizes, and explains actions.
- Orientation from yourself when determining the direction of movement (with change) through the labyrinth.
Low level.
He leads with a pencil, but does not indicate the direction. Makes several attempts.
Average level.
Names changes in the direction of movement, makes mistakes. Explains his actions.
High level.
Accurately identifies and names directions.
- The ability to alternate and distribute objects (by color, shape, quantity); practically focus on the algorithm specified verbally, performing actions based on a visual basis (drawing).
Low level.
The target of the action is not aware. Performs chaotic actions.
Average level.
Carries out actions according to the picture, adheres to the goal, explains. The result is only partially achieved.
High level.
Solve problems correctly and offer options. Explains.
- Manifestation of guesswork and ingenuity when solving logical problems included in a situation-game.
Low level.
Reflects everyday understanding of the situation.
Average level.
Offers guesses, tells stories, makes mistakes.
High level.
Completes the task mentally, proves the correctness of the decision.
- Emotional attitude to the proposed tasks. An outward expression of interest.
Low level.
Indifferent, interested in pictures.
Average level.
Rejoices at success.
High level.
Tries to analyze his actions, asserts their correctness. Rejoices at success.
The procedure for carrying out diagnostics, explanations of tasks, types of possible assistance, for each task may have its own characteristics.
Before diagnosis, children should be familiarized with similar tasks.
- The examination is carried out in the first half of the day from 9 to 12 o'clock, on Tuesday or Wednesday, when the maximum level of children's performance during the week is observed.
- The examination is carried out in a calm, supportive environment.
- Only one specialist (either a teacher or a psychologist) works with a child at a time; this is due to the fact that cross-examination of several adults often makes contact difficult and does not allow obtaining objective results.
- If a more in-depth examination by specialists (speech therapist, psychologist) is necessary, it is more advisable to do this at another time.
- All necessary supplies, manuals and materials are not lying on the table at which the child will work; they are laid out in a certain order on a separate table.
- Parents can be present during the examination; it is advisable for them to sit with their backs to the child. (This time can be used for parents to answer survey questions.)
During the examination, teachers:
- do not rush the child, do not rush with a hint;
- do not show their displeasure or dissatisfaction;
- do not emphasize negative results and analyze the results together with the parents in the presence of the child.
3. Methods for reporting diagnostic results
To correctly determine the level of mathematical preparation, it is necessary to diagnose the entire proposed set of tasks and draw conclusions based on the total result. This is important for further correction in order to select those tasks that the child cannot cope with.
Design methods may vary. Most often, levels are assigned a certain number of points. For example, a low level is from 1 to 3 points, an average level is from 4 to 6 points, a high level is from 7 to 9 points. Each level is allocated a certain number of points. To assign points, you must carefully observe the test taker’s performance of the task and record his actions, behavior, attitude to the task, speech and other parameters that determine the level in this task. To record the parameters, you can use pre-prepared forms in which the parameters are indicated, and the teacher, watching the child complete the task, makes notes on the form. Various tables are used to record the completion of each task operation.
It is important that each test task is assessed and the result recorded. After evaluating each completed task, the results in points for each task are recorded in a summary table. Based on the result of the total score, a conclusion is made about the level of mathematical development of each child and a form is drawn up for recording individual results for the entire test. After that, a form for group registration of test results is drawn up. The forms indicate where, when, for what purpose the test was conducted and what content it was, how many children were tested, and what skills the tasks were aimed at identifying. We draw conclusions individually for each child and in general about the entire tested group. This is important in order to identify pedagogical omissions (in case the majority of children did not cope with the same task).
4. Taking into account diagnostic results in pedagogical work with children
The diagnostic results allow the teacher to more accurately and completely take into account the individual characteristics of each child. If the pedagogical influence is built taking into account the level of development achieved at the previous stage of the child’s life, and is based on the strengths of his personality, then this influence ensures the successful inclusion of the child in educational and cognitive activities, contributes to the formation of a positive attitude towards this activity, and significantly influences the formation of diligence, hard work, activity. And also, taking into account diagnostic results stimulates the development of basic mental processes and ensures the correct construction of special corrective measures.
Without taking into account the diagnostic results, the initial developmental deviations only worsen, which will be almost impossible to compensate in the future.
Correctional and developmental education is built taking into account the diagnostic results in order to pay increased attention from the teacher to the development of those mental processes, the formation of which in a given child is either somewhat delayed or does not quite correspond to our approximate ideas about the norm of development. The diagnostic results make it possible to determine the nature of the goal of correctional and developmental work in mathematics classes. The nature of the goal could be as follows:
— intellectual-perceptual
: correction and development of adequate perception of information presented visually and auditorily; correction and development of skills of an analytical nature - essential characteristics, separation of the main from the secondary, identification of patterns, distribution according to the selected characteristics (classification) and generalization of the results of activity (in subject-practical or verbal form);
— regulatory-dynamic
: formation of elements of educational and cognitive activity - understanding of the assigned educational task, independent selection of the necessary means in accordance with the task, activity planning and self-analysis (the ability to find and correct errors), stimulation of educational and cognitive motivation, cognitive interest and educational independence;
— psychophysiological
: development, correction or compensation of disturbances in the activity of analyzers, development of fine motor skills, kinesthetic sensitivity, spatial coordination.
The diagnostic results are taken into account when assessing the level of professional competence of the teacher, in order to provide timely assistance in mastering the necessary techniques.
Practical part:
1. To examine the level of development of mathematical concepts of older preschoolers and give pedagogical recommendations
Express diagnostics of the cognitive development of preschool children and the level of development of mathematical concepts in children of senior preschool age.
Diagnosis was carried out on the basis of a kindergarten. In total, the study involved 25 children aged 5 years 4 months - 5 years 10 months.
Example 1
. "Organizing"
Purpose of the task.
To identify children’s understanding of counting objects and their ordering.
Materials.
Cardboard circles with a diameter of 5 cm with dots. The circles are placed in front of the child in disorder.
Exercise.
In some circles there are few dots, in others there are many. Now the circles are in disarray. Think and arrange these circles in a row in order. When you look for this or that order, do not forget that there are points on the circles.
Execution method.
You should not tell your child the principle of ordering. Completing the task independently will show the level of formation of his idea of orderliness.
Assignment rating:
Level 1 - the task was completed completely correctly;
Level 2 - 1-2 mistakes were made;
Level 3 – 3-4 mistakes were made;
Level 4 – more than 5 mistakes were made.
Example 2.
"Primary mathematical concepts"
Purpose of the task.
Determine children’s understanding of ratios:
more by, less by;
about quantitative and ordinal counting, about the shape of the simplest geometric figures.
Materials.
Seven of any objects or their images on a flannelgraph; the objects can be either the same or different.
Execution method.
To complete the task, the child is given a piece of paper and a pencil. The task consists of several parts. They are offered sequentially.
Tasks.
A
. Draw as many circles on the sheet as there are objects on the board.
B.
Draw one more squares than circles.
IN.
Draw two fewer triangles than circles.
G.
Draw a line around six squares.
D.
Fill in the fifth circle.
Assignment assessment
(the quality of performance of all tasks in total is assessed):
Level 1 - the task was completed completely correctly;
Level 2 - 1-2 mistakes were made;
Level 3 – 3-4 mistakes were made;
Level 4 – more than 5 mistakes were made.
Example 3
Purpose of the task.
Conduct diagnostics of the ability to analyze the conditions of the presented task, in this case of a practical nature (plan the course of its solution, choose adequate actions, critically evaluate the result obtained). The task also determines the visual adequacy of determining the shape of a figure, spatial mobility of thinking - the ability to mentally move and arrange parts, and the adequacy of visual assessment of the size of figures.
Materials.
A white sheet of paper with an image of the outline of a boat with a sail and colored geometric shapes: 4 squares 2x2 cm, 4 right isosceles triangles with a leg 2 cm, all the same color.
2 cm
6cm
Exercise.
Part 1
. “Color” the boat, but not with pencils, but with these figures. The figures must be placed inside the boat so that they do not extend beyond the image.
Part 2.
Evaluate the quality of the task - was everything done correctly? If the child himself does not notice the mistakes made (the figures do not fit together, they go beyond the outline), the teacher asks if the child wants to make a new boat better than this one. If the answer is negative, the teacher does not insist on it.
Assessment of the task.
A
The method of completing the task is assessed: whether the child first thought about its implementation, planned it, or worked without any system, by trial and error.
B.
The rationality of the placement of figures is assessed.
IN
.Criticality in assessing task performance is assessed.
G
. The desire and readiness to correct mistakes is assessed.
D.
The pace of activity is assessed.
1st level - the figures are laid out correctly and quickly (the child instantly analyzed the task and began to complete it);
Level 2 - the outline is filled out correctly, but the child worked by trial and error, so he spent more time; corrected himself in the process of work;
3rd level - only part of the outline is filled correctly, some figures go beyond its outline; when evaluating work, the child does not notice mistakes, but when the teacher draws his attention to them, he is ready to correct them;
Level 4 - the outline is filled chaotically, most geometric shapes go beyond its outline, errors are not noticed, and there is no desire to do better when pointing them out.
Example 4.
"Checking in the house"
Purpose of the task.
Identify children’s ability to consider a situation from different angles, the ability to switch from one solution found to the search for another.
Materials.
A house is drawn in advance on a board or on a large sheet of paper,
cards with large images of the “tenants” of the house; Each child is given a sheet of paper with a picture of the same house and a felt-tip pen.
Exercise.
Part 1 (educational).
The house has six floors. There are three rooms on each floor. Each room has one resident: the teacher shows the images - a dot, a stick and a tick. On all floors they live in different orders. On the top floor in the first room on the left there is a dot (draws a dot in the window), in the middle room there is a wand (draws a wand).
- Tell me who lives in the last room? (The children name a tick, and the teacher draws it.) Now draw on your piece of paper who lives where on the sixth floor. (Children draw, the teacher checks the correctness of the drawing.)
- Now we will populate the fifth floor with residents: a dot also lives in the first room. Think about how you need to house the wand and the tick so that they do not live in the same order as on the sixth floor. The placement of the “tenants” is drawn in the windows of a large house, and then the children draw them in their own homes. This concludes the training part of the task.
Part 2 (main).
- There are still four floors left. Populate them yourself so that on each floor there lives one dot, one stick and one tick, but in a different order. Children complete the task independently.
Assessment of the task.
1st level - the task was completed correctly: all 4 accommodation options were found that do not repeat the “occupancy” of the fifth and sixth floors;
2nd level - 2-3 different placement options were found out of four possible;
Level 3—one placement option out of four possible has been found;
Level 4 - no independent solutions were found: the solutions from the training stage were repeated or the work was not completed (the floors remained uninhabited).
Example 5.
Coloring shapes
Purpose of the task.
Demonstrate the ability to classify visual material according to an independently found basis.
Determine the degree of adequacy of visual perception of form and the ability to mentally move and combine figures to determine their equality. Materials.
Each child receives a drawing with a number of figures, felt-tip pens or pencils.
Exercise.
Identical figures must be painted with the same color. The color is chosen independently. The number of groups of identical figures the child finds, the number of colors he uses.
Assessment of the task.
1st level - classification is done correctly; three groups of different figures are identified (3 isosceles triangles, 4 equilateral and 3 rectangular).
Level 2 - one error (failure to distinguish identical figures in a straight and rotated position; or failure to distinguish identical figures in a straight and mirror position);
Level 3 - two errors (not distinguishing identical figures in direct and rotated positions and not distinguishing figures in direct and mirror positions);
Level 4 - three errors (failure to distinguish identical figures in a straight and rotated position, in a straight and mirror position, and also failure to distinguish between different figures); senseless, chaotic coloring of figures.
results
express diagnostics of the cognitive development of preschool children and the level of formation of mathematical concepts of children of senior preschool age in the senior group of kindergarten
Example 1
. "Organizing"
| I.F. | level | I.F. | level | I.F. | level |
| A.Sh. | IV | VC. | II | M.D. | I |
| A.Z. | I | D.V. | I | N.Z. | II |
| A.K. | I | D.D. | III | N.P. | II |
| A.P. | III | D.L. | I | O.V. | II |
| A.Le. | I | YES. | I | THOSE. | II |
| A.L. | I | Z.R. | I | T.A. | I |
| A.M. | II | K.B. | I | Yu.Z. | I |
| V.D. | I | K.N. | I | ||
| V.N. | II | L.S. | I |
Example 2.
"Primary mathematical concepts"
| I.F. | level | I.F. | level | I.F. | level |
| A. Sh. | III | VC. | II | M.D. | I |
| A.Z. | I | D.V. | II | N.Z. | I |
| A.K. | I | D.D. | III | N.P. | I |
| A.P. | III | D.L. | I | O.V. | III |
| A.Le. | I | YES. | II | THOSE. | II |
| A.L. | I | Z.R. | I | T.A. | II |
| A.M. | I | K.B. | I | Yu.Z. | I |
| V.D. | III | K.N. | I | ||
| V.N. | I | L.S. | II |
Example 3.
| I.F. | level | I.F. | level | I.F. | level |
| A.Sh. | III | VC. | II | M.D. | I |
| A.Z. | I | D.V. | II | N.Z. | I |
| A.K. | I | D.D. | III | N.P. | I |
| A.P. | IV | D.L. | II | O.V. | II |
| A.Le. | I | YES. | II | THOSE. | II |
| A.L. | I | Z.R. | I | T.A. | II |
| A.M. | I | K.B. | I | Yu.Z. | II |
| V.D. | III | K.N. | I | ||
| V.N. | II | L.S. | II |
Example 4.
"Checking in the house"
| I.F. | level | I.F. | level | I.F. | level |
| A.Sh. | III | VC. | I | M.D. | I |
| A.Z. | II | D.V. | I | N.Z. | I |
| A.K. | I | D.D. | III | N.P. | II |
| A.P. | IV | D.L. | III | O.V. | III |
| A.Le. | II | YES. | I | THOSE. | I |
| A.L. | II | Z.R. | II | T.A. | I |
| A.M. | II | K.B. | II | Yu.Z. | II |
| V.D. | I | K.N. | II | ||
| V.N. | II | L.S. | I |
Example 5.
Coloring shapes
| I.F. | level | I.F. | level | I.F. | level |
| A.Sh. | II | VC. | I | M.D. | II |
| A.Z. | I | D.V. | II | N.Z. | II |
| A.K. | II | D.D. | II | N.P. | II |
| A.P. | II | D.L. | I | O.V. | III |
| A.Le. | I | YES. | II | THOSE. | I |
| A.L. | I | Z.R. | I | T.A. | I |
| A.M. | I | K.B. | II | Yu.Z. | II |
| V.D. | I | K.N. | II | ||
| V.N. | I | L.S. | I |
Pivot table
| Example 1 | Example 2 | Example 3 | Example 4 | Example 5 | Bottom line | |
| A.Sh. | IV | III | III | III | II | 15 |
| A.Z. | I | I | I | II | I | 6 |
| A.K. | I | I | I | I | II | 6 |
| A.P. | III | III | IV | IV | II | 16 |
| A.Le. | I | I | I | II | I | 6 |
| A.L. | I | I | I | II | I | 6 |
| A.M. | II | I | I | II | I | 7 |
| V.D. | I | III | III | I | I | 9 |
| V.N. | II | I | II | II | I | 8 |
| VC. | II | II | II | I | I | 8 |
| D.V. | I | II | II | I | II | 8 |
| D.D. | III | III | III | III | II | 14 |
| D.L. | I | I | II | III | I | 8 |
| YES. | I | II | II | I | II | 8 |
| Z.R. | I | I | I | II | I | 6 |
| K.B. | I | I | I | II | II | 7 |
| K.N. | I | I | I | II | II | 7 |
| L.S. | I | II | II | I | I | 7 |
| M.D | I | I | I | I | II | 6 |
| N.Z. | II | I | I | I | II | 7 |
| N.P. | II | I | I | II | II | 8 |
| O.V. | II | III | II | III | III | 13 |
| THOSE. | II | II | II | I | I | 8 |
| T.A. | I | II | II | I | I | 7 |
| Yu.Z. | I | I | II | II | II | 8 |
Let us determine the level of cognitive development and formation of mathematical concepts of preschoolers.
High: 5-7 points
Average: 8-11 points
Low: 12 points or less.
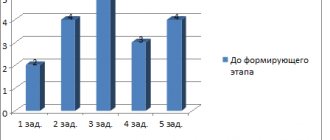
Among the tested, 12 children were found to have a high level, 9 children an average level and 4 children a low level of cognitive development and the formation of mathematical concepts.
Recommendations: the tasks of the first three examples test the level of development of mathematical concepts of spatial and constructive thinking, and the last two reveal the level of development of the mathematical style of thinking. Consequently, children with an identified low level of cognitive development and the formation of mathematical concepts need correction using tasks that develop spatial and constructive thinking, as well as those aimed at developing a mathematical thinking style. After carrying out a set of corrective classes, repeated diagnostics are necessary. If a positive effect is not achieved, a more in-depth psychological diagnosis is recommended.
Literature:
- Beloshistaya A.V. Formation and development of mathematical abilities of preschool children: Issues of theory and practice. A course of lectures for students of preschool faculties of higher educational institutions. – M: Humanitarian Publishing Center VLADOS, 2003.- 400 p.
- Mathematical development of preschool children: Educational and methodological manual/Compiled. Z.A.Mikhailova, M.N.Polyakova, R.L.Nepomnyashchaya, A.M.Verbenets - St. Petersburg: Detstvo-Press, 2000. - 94 p.
- Mikhailova Z.A., Nosova E.A. et al. Theories and technologies of mathematical development of preschool children. – St. Petersburg: “Childhood-Press”, 2008. – 384 p., illus.
- https://adalin.mospsy.ru/l_01_00/l_01_08e.shtml
To carry out diagnostics, informal test tasks are most often used, revealing the child’s current level of mastery of geometric figures, size parameters, skills to count and compare groups of objects by number, compose (practically) numbers from two smaller ones within 10, solve simple logical and arithmetic problems, etc. .d. With this approach to diagnostics, the mastery of the content specified in the program is mainly checked.
Other approaches to diagnosis are possible, for example, assessing mathematical development from the perspective of the child’s logical-mathematical experience, which includes mastering the actions (methods) of cognition and means of cognition.
Depending on the age of children, the following methods of cognition are subject to assessment: examination, comparison, equalization, counting, measurement with conventional standards, experimentation, transformation and reconstruction, modeling, etc. Among them, the most significant in terms of logical cognition can be identified: grouping and classification, ordering and seriation.
The means of cognition include sensory standards (color, shape), conventional measures (samples for comparison, comparison by size, mass, volume), images (ideas about spatial and temporal relationships, changes, numbers, quantities), models, speech.
Purpose of diagnosis
will consist of tracking achievements in a 5-6 year old child’s mastery of both means and methods of cognition.
Based on the results obtained, his logical-mathematical experience is determined, which is represented by a propensity (or lack thereof) for independent cognition, manifestation of activity in search and creative gaming activities, the ability to use mastered means and actions in order to independently discover the truth, simple connections and dependencies of groups of objects by properties (shape, size, mass, volume, location) and relations of correspondence and similarity, order (ordinal dependence), parts and the whole.
The process of interaction between an adult and a 5-6 year old child in a diagnostic situation will constitute the object of diagnosis.
The subject of diagnostics, aimed at identifying the logical and mathematical experience of a child, is the child’s training, his activity skills, interests and inclinations.
As a result, the child’s behavior in a cognitive situation will be revealed, the degree of manifestation of independence (starts to perform; asks, waits for help; doubts, says that he cannot cope) and specific skills to operate with numbers, simple schematic images and models, combine and decode.
An indispensable condition for choosing or developing diagnostics for the mathematical development of children is its compliance with the educational program being implemented.
The provisions set out in this paragraph about the purpose of diagnosing the mathematical development of children (identifying logical-mathematical experience), its focus on assessing the level of cognitive and personal development, activity and independence of children, the ability to express in speech methods of practical activity, connections and dependencies gives grounds for classifying it to the program “Childhood” (section “First steps in mathematics”).
Such an approach to diagnosing the mathematical development of preschool children involves, to a greater extent, identifying the levels of mental development achieved, including in mastering logical and mathematical content, rather than specific skills in the practical operation of figures, quantities, and numbers.
In our opinion, this position does not conflict with the conceptual ideas of the section “First steps in mathematics” of the “Childhood” program, which is designed based on the principles of the theory of developmental learning and modern pedagogical technologies for the development and training of preschool children.
Using the example of diagnostics of mathematical development of children 5-6 years old, developed by Z.A. Mikhailova and I.N. Cheplashkina, we will consider the basic requirements for organizing the diagnostic procedure.
The form of organizing a diagnostic examination is problem-game situations, which include cognitive tasks.
The initial (initial diagnosis) is carried out at the beginning of the school year (at the end of September) and consists of three situations: “Who is not drawn in the picture?”, “Enter the hut”, “Restore the ladder”.
Diagnostic situation “Who is not drawn in the picture?”
The child is presented with a logical task with an incomplete set of pictures. Instead of one missing picture, as is usually the case in such problems, there are three. An example is the second row, where what is said in the situation is drawn: Christopher Robin drew his friends, Eeyore, Winnie the Pooh and Piglet, in different ways: cheerful - with slitted eyes, surprised - with round eyes, scared - with square eyes. The friends looked at the artist’s drawings and took the best ones.
Instructions: “Look at the picture and tell me who took the pictures and which ones?
(Children use answer options.) Can you prove who exactly took these drawings?”
During the decision, it is important to understand and remember: who is drawn (donkey, bear and pig), how (with slits, round and square eyes). The combination of features is unknown: the name of the animal, its inherent eye shape, location (three features). To practically search for answers, you need to cut the second (drawn on the right) picture, arranging the resulting squares in the same order.
To search for portraits that have already been taken, and those who took them, you should “uncover” the pattern that each row and column contains all three features: different animals, with three eye patterns, with different locations in space.
When solving this problem, the child practically chooses portraits that have already been taken. In the top row is a portrait of a bear cub, but with square eyes; in the third (bottom) row on the left - a bear cub with slitted eyes and on the right - a donkey with round eyes.
Diagnostic tasks:
identify children’s ability to compare and generalize based on signs of similarity and difference, independently “discover” for themselves the rules for constructing a logical problem (which figure to put where), reason, detect and correct errors.
Naturally, it is possible to complete the assigned diagnostic tasks only under the condition of friendly communication between an adult and a child, confirmation of both correct answers and doubts, avoiding direct prompts.
Diagnostic situation “Enter the hut”
The goal involves identifying the practical skills of children 5-6 years old in composing numbers from two smaller ones and in carrying out search actions.
On three huts located in a row, the numbers (6, 9, 7, respectively) indicate the number of gold coins. Traces lead to the huts. Only the one who opens the door can take the coins. To do this, you need to step on the left and right footprints together as many times as the number shows. (Mark with pencil.)
Teacher: “Which hut did you choose? What tracks will you step on? Check if the door will open? If you want, then enter other huts.”
Diagnostic situation “Let’s restore the ladder”
The goal is to identify skills to detect violations (errors) in the order of objects in height, restore rows, and explain errors based on establishing the correspondence of objects in height and serial number.
The name of the situation “Restore the ladder” indicates the game orientation and the implementation of a number of actions.
The ladder of Cuisenaire’s counting sticks is made with the passage of the “6” stick on the ascent and the “5”, “4”, “2” sticks on the descent. To carry out diagnostics, you can use a drawing, but it is advisable to make a ladder on a plane and put the missing sticks, among which there should be “extra” ones.
Instructions. Hungry, curious mice smelled the cheese, but couldn’t climb the steps to get it. Name the numbers of the steps that the skinny mouse is going to climb. Which step in order is missing in his ladder? Can you fix the ladder? Fix it!
Name the numbers of the steps that the fat mouse is going to climb. What steps in order are missing in his ladder? Name it. Help him too! Now he can enjoy cheese? Is it comfortable to walk up the stairs now?
So, three situations that can be presented to a child of the sixth year of life will help the teacher to navigate how children relate to such situations, whether they are interested in them, what level of mental activity they show in this case, what their skills are to compare and use the results when solving cognitive problems. tasks, understand simple patterns of alternation, sequence, establish the relationship between numbers and numbers, compose numbers from two smaller ones, establish the order of quantities and numbers.
At the end of the school year, diagnostics are carried out again, also represented by three game situations. Children's age is 5 years 8 months—6 years.
Diagnostic situation “Correct the mistakes and name the next move”
The goal is to identify children’s abilities to follow the rules of the sequence of moves, offer options for correcting mistakes, reason, and mentally justify the course of their actions.
The situation is being organized without practical action. The child watches the adult’s progress, comments on his own move, and corrects mistakes.
Instructions. Imagine that you and I are playing dominoes. Some of us made mistakes. Find them and fix them. The first move was mine (left). As mistakes are discovered, the child is asked the question: “Which of us made mistakes? How can I fix them using additional chips?”
Diagnostic situation “Which days are missed?”
The goal is to identify children’s ideas about the sequence of days of the week, the ability to justify the order of the days of the week, and to restore missed days (in game conditions).
Instructions. Take a look at this calendar. This is four weeks. Let's determine what the children do on the first day of the week, Monday (music class), Tuesday (mathematics) on the second, etc. Look at the second week and tell me which days are missing. Give their serial numbers. Third week. Consider this. If it is Friday (show), then which 2 days are missing? Fourth week. Is it a full week?
Diagnostic situation “Whose backpack is heavier?”
The goal is to identify children’s skills in using methods for determining mass, comparing objects, explaining their train of thought, and using the words: “heavier,” “lighter,” “weighs the same.”
Instructions: look at the backpacks with fruit. (Who is carrying them? Where are they going? What is in the backpacks?)
What are the scales for in the picture? What is the weight of one pear?
“Weigh” fruits on scales using apples instead of weights. Determine the heaviest backpack, the lightest one. (You can use a pencil.)
So, during the final (at the end of the school year) diagnostics, the teacher identifies children’s abilities to act and think consistently on different contents: when navigating in the game “Dominoes”, in the days of the week, in the process of correlating one quantity with another when estimating mass. These requirements correspond to the capabilities of 6-year-old children and the tasks of the “First steps in mathematics” section of the “Childhood” program.
What should be assessed at the end of the diagnosis?
The teacher evaluates the effectiveness of his teaching activities: how active the child is, how smart he is, whether he understands the task posed in the situation, whether he is involved in search activities, whether he is reasoning about the result obtained or a mistake made, whether he is going in the right direction, whether he supports the dialogue started by an adult, whether he is fluent. necessary actions (comparisons, generalizations, measurements, etc.).
When summing up the diagnostic results, one should take into account the results of everyday short-term observations of the child, his behavior in a new unknown game, in a creative or problematic situation.
It is advisable to analyze the results according to the following indicators:
mastery of practical actions (methods of cognition) of the properties and relationships of both individual objects and groups in shape, size, quantity, mass; based on the identification of spatial and temporal relationships (at the sensory, elementary logical levels);
mastery of the skills to identify connections, dependencies, compare, alternate, establish and change sequences, model, schematize;
mastering the ability to express in speech the essence of practical actions and predictable ones (“how I will do”): measurement, dividing the whole into parts, increasing and decreasing in size, numbers, etc.;
manifestation of initiative in logical and mathematical activities, elements of search, experimentation, creativity - both in specially organized situations and in life situations that arise spontaneously.
Based on taking into account these indicators, it is possible to characterize the child’s logical and mathematical experience.
The teacher should take a responsible approach to identified deficiencies in the development of children:
analyze the subject-game development environment;
to initiate the creative cognitive activity of individual children on the basis of personal participation in their activities, the creation of play communities, and the use of motivation that is meaningful to them;
induce in children a desire to tell their parents about their successes in the group, about joint actions with peers and the teacher; select games, gaming materials necessary for independent mastery of actions that are especially necessary in a given period (knowledge of the dependencies between numbers, quantities in the conditions of a serial series);
practice organizing and conducting leisure activities, children's games, projects, joint events with parents, which will help increase activity in general.